9  Problems 1

Week 2

These problems sheets are designed to help you learn mechanics. You get better at physics by solving problems. You will attempt these questions at the problems class. This means you do not need to complete the problems beforehand, but it might be helpful to have looked over them. Your solutions will not be marked. Solutions will be provided on Blackboard the week following your problems class. If you are using these for revision try to do the questions first without looking at the answers.

9.1 Projectile motion

A particle is launched with speed \(u\) at an angle \(\theta\) to the horizontal. The particle experiences a constant acceleration in the vertical direction due to gravity, \(g\).

  1. What are the \(x\) and \(y\) components of the particle’s initial velocity?
  2. What is the maximum height of the projectile?
  3. How long does it take the particle to return to the ground?
  4. What is the range of the particle?
  5. Differentiate your answer to part (d) to show that the maximum range of the particle is achieved when \(\theta = 45^\circ\).

The \(x\) and \(y\) components of the particle’s initial velocity are \[ u_x = u \cos \theta \] \[ u_y = u \sin \theta \]

We only need to consider the vertical motion. There is constant acceleration so we can use the “SUVAT” equations. We can use the “\(v^2 = u^2 + 2as\)”” equation. The final velocity is zero at the maximum height, so \[ 0 = u_y^2 + 2(-g)s \] \[ s = \frac{(u \sin \theta)^2}{2g} \]

The particle returns to the ground when its vertical displacement is zero. We can use the “\(s = ut + \frac{1}{2}at^2\)” equation. \[ s = u_y t - \frac{1}{2}gt^2 \] \[ 0 = u \sin \theta t - \frac{1}{2}gt^2 \] \[ t = 0 \text{ or } t = \frac{2u \sin \theta}{g} \]

The range is the horizontal displacement of the particle. We can use the “\(s = ut + \frac{1}{2}at^2\)” equation with the time we have calculated above. There is no horizontal acceleration. \[ R = u_x t \] \[ = u \cos \theta \times \frac{2u \sin \theta}{g} \] \[ = \frac{2u^2 \sin \theta \cos \theta}{g} \] \[ = \frac{u^2 \sin 2\theta}{g} \] where we have made use of the double angle formula for \(\sin 2\theta = 2 \sin \theta \cos \theta\).

We have calculated the range as a function of inclination angle, \(R(\theta)\). We want to find the value of \(\theta\) that maximises the range. We do this by differentiating \(R(\theta)\) with respect to \(\theta\), and setting this to zero. \[ \frac{dR(\theta)}{d\theta} = \frac{d}{d\theta} \left( \frac{u^2 \sin 2\theta}{g} \right) \] \[ = \frac{u^2}{g} 2 \cos 2\theta = 0 \] \(\cos 2\theta = 0\) when \(2\theta = 90^\circ\), i.e. when \(\theta = 45^\circ\).

9.2 Vector addition

Vectors whose moduli are 3, 4, and 6 act in directions making angles \(30^\circ\), \(90^\circ\), and \(135^\circ\) respectively with the positive \(x\)-axis, and all lie in the \(x - y\) plane. Find their sum. Give the modulus and direction of the resultant vector.

  • One way to do this is to work out the \(\vec{\imath}\) and \(\vec{\jmath}\) components of each vector, then add them together.
  • “Modulus” is another word for “magnitude”.

We can find the components of each vector parallel to the \(x\) and \(y\)-axes. \[ \vec{v}_1 = 3 (\cos 30^\circ \hat{\imath} + \sin 30^\circ \hat{\jmath}) = 2.598 \hat{\imath} + 1.5 \hat{\jmath} \] \[ \vec{v}_2 = 4 (\cos 90^\circ \hat{\imath} + \sin 90^\circ \hat{\jmath}) = 0 \hat{\imath} + 4 \hat{\jmath} \] \[ \vec{v}_3 = 6 (\cos 135^\circ \hat{\imath} + \sin 135^\circ \hat{\jmath}) = -4.243 \hat{\imath} + 4.243 \hat{\jmath} \] Sum these to get the resultant vector \[ \vec{R} = \vec{v}_1 + \vec{v}_2 + \vec{v}_3 = -1.645 \hat{\imath} + 9.743 \hat{\jmath} \] The modulus is given by \[ |\vec{R}| = \sqrt{(-1.645)^2 + (9.743)^2} = 9.88 \text{ N} \] and the direction is given by \[ \theta = \tan^{-1} \left( \frac{9.743}{-1.645} \right) = 99.6^\circ \]

9.3 Angles between vectors

The resultant, \(\vec{R}\), of two intersecting forces \(\vec{F}_a\) and \(\vec{F}_b\) has magnitude \(\sqrt{3} \text{ N}\). If \(|\vec{F}_a| = 1 \text{ N}\) and \(|\vec{F}_b| = 2 \text{ N}\), find the angle between \(\vec{F}_a\) and \(\vec{F}_b\), and the angle between \(\vec{F}_a\) and \(\vec{R}\).

  • Draw a diagram.
  • Use the cosine rule, and the sine rule.

Use the cosine rule to find the angle between \(\vec{F}_a\) and \(\vec{F}_b\) \[ |\vec{R}^2| = |\vec{F}_a|^2 + |\vec{F}_b|^2 - 2 |\vec{F}_a| |\vec{F}_b| \cos \theta \] i.e., \[ 3 = 1 + 4 - 4 \cos \theta \] and so \(\theta = 60^\circ\). From your diagram you want the exterior angle which is \(120^\circ\). For the angle \(\phi\) between \(\vec{F}_a\) and \(\vec{R}\) use the sine rule \[ \frac{2}{\sin \phi} = \frac{\sqrt{3}}{\sin 60^\circ} \] Hence \(\sin \phi = 1\) and \(\phi = 90^\circ\).

9.4 Non-uniform acceleration with vectors & derivatives

A particle of mass \(m = 2 \text{ kg}\) is acted on by a force \(\vec{F}\) in newtons. The position \(\vec{r}\) of the particle is found to follow a path due to this force given by \[ \vec{r} = \left( \frac{5t^2}{3b} - \frac{t^3}{4c} \right) \hat{\imath} + \left( \frac{3t^2}{b} - \frac{7t}{a} \right) \hat{\jmath} \text{ m} \] where \(a\), \(b\) and \(c\) are constants with the value 1 in appropriate units, when distance is measured in metres and time in seconds. Find the following.

  1. The units of the constants \(a\), \(b\) and \(c\).
  2. The value of \(t\) when the particle is moving parallel to the vector \(\hat{\imath}\).
  3. The force \(\vec{F} = m \vec{a}\), where \(\vec{a}\) is the acceleration, after 5 seconds.
  4. The magnitude of the force determined in part (c).

The units of the constants \(a\), \(b\) and \(c\) are found by considering the units of the position \(\vec{r}\) and time \(t\).

The position \(\vec{r}\) has units of metres, and time \(t\) has units of seconds. Therefore, the units of the constants \(a\), \(b\) and \(c\) are: \[ \text{Units of } b = \text{ m}^{-1}\text{ s}^2 \] \[ \text{Units of } c = \text{ m}^{-1}\text{ s}^3 \] \[ \text{Units of } a = \text{ m}^{-1}\text{ s} \]

To get the velocity we need to differentiate \(\vec{r}\) with respect to time, \[ \vec{v} = \frac{d\vec{r}}{dt} = \left( \frac{10t}{3b} - \frac{3t^2}{4c} \right) \hat{\imath} + \left( \frac{6t}{b} - \frac{7}{a} \right) \hat{\jmath} \text{ m s}^{-1} \] \(\vec{v}\) will be parallel to \(\hat{\imath}\) when the \(\hat{\jmath}\) component is zero. This occurs when \[ \frac{6t}{b} - \frac{7}{a} = 0 \] \[ t = 1.17 \text{ s} \]

The acceleration is the derivative of the velocity with respect to time, \[ \vec{a}(t) = \frac{d\vec{v}}{dt} = \left( \frac{10}{3b} - \frac{6t}{4c} \right) \hat{\imath} + \left( \frac{6}{b} \right) \hat{\jmath} \text{ m s}^{-2} \] The acceleration after 5 seconds is \[ \vec{a}(t = 5) = \left( \frac{10}{3} - \frac{30}{4} \right) \hat{\imath} + \left( 6 \right) \hat{\jmath} = -4.17 \hat{\imath} + 6 \hat{\jmath} \text{ m s}^{-2} \] The force after 5 seconds is \[ \vec{F}(t = 5) = m \vec{a}(t = 5) = -8.33 \hat{\imath} + 12 \hat{\jmath} \text{ N} \]

Use Pythagoras’ theorem to find the magnitude of the force, \[ |\vec{F}| = \sqrt{(-8.33)^2 + (12)^2} = 14.6 \text{ N} \]

9.5 Centre of mass of system of particles in 3D

Particles 1,2,3 with mass \(m_1 = 3 \text{ kg}\), \(m_2 = 6 \text{ kg}\) and \(m_3 = 7 \text{ kg}\) are located at positions defined by the vectors \(\vec{r}_1 = 5\hat{\imath} - 7\hat{\jmath} \text{ m}\), \(\vec{r}_2 = 3\hat{\imath} + 6\hat{\jmath} \text{ m}\) and \(\vec{r}_3 = 7\hat{\imath} + 3\hat{\jmath} \text{ m}\).

  1. Determine the position of the centre of mass of the three-particle system.
  2. The particles are subsequently displaced in the direction of \(\hat{k}\) so that their new positions are given by \(\vec{r}^\prime_1 = 5\hat{\imath} - 7\hat{\jmath} + 3\hat{k} \text{ m}\), \(\vec{r}^\prime_2 = 3\hat{\imath} + 6\hat{\jmath} + 6\hat{k} \text{ m}\) and \(\vec{r}^\prime_3 = 7\hat{\imath} + 3\hat{\jmath} - 3\hat{k} \text{ m}\). Determine the new position of the centre of mass of the particle system.
  3. If this translation occurs uniformly over a time \(t\), what is the velocity of the centre of mass frame?

Here we use \[ \sum_{i=1}^3 m_i \vec{r}_i = \vec{r}_\text{com} \sum_{i=1}^3 m_i \] \[ \vec{r}_\text{com} = \frac{\sum_{i=1}^3 m_i \vec{r}_i}{\sum_{i=1}^3 m_i} \] \[ = \frac{3 \times (5\hat{\imath} - 7\hat{\jmath}) + 6 \times (3\hat{\imath} + 6\hat{\jmath}) + 7 \times (7\hat{\imath} + 3\hat{\jmath})}{3 + 6 + 7} \text{ m} \] \[ = \frac{41}{8}\hat{\imath} + \frac{9}{4}\hat{\jmath} \text{ m} \]

The \(\hat{\imath}\) and \(\hat{\jmath}\) components are unaffected so that the \(\hat{k}\) component becomes \((3 \times 3 + 6 \times 6 - 7 \times 3)/16 = 24/16 = 3/2\). Hence the new centre of mass is \[ \vec{r'}_\text{com} = \frac{41}{8} \hat{\imath} + \frac{9}{4} \hat{\jmath} + \frac{3}{2} \hat{k} \text{ m} \]

If we assume the displacement takes place uniformly over a time \(t\), then the velocity of the centre of mass is \[ \vec{v}_\text{com} = \frac{\vec{r'}_\text{com} - \vec{r}_\text{com}}{t} \] \[ = \frac{3}{2t} \hat{k} \text{ m s}^{-1} \]

9.6 Bonus question: Galilean transformation using vectors

Galileo reputedly tested his ideas about Galilean relativity and gravity by dropping objects from the leaning tower of Pisa, which has height \(56 \text{ m}\).

  1. Assume Galileo dropped a book of mass \(2.4 \text{ kg}\) from the tower. Write down a vector equation for the book’s position as a function of time in Galileo’s frame, i.e. take Galileo to be the origin, and a gravitational force proportional to \(g\) in the \(-\hat{k}\) direction, and ignore the effects of wind resistance.
  2. A bird was flying near Galileo as he dropped the book, with instantaneous position \(3.1 \hat{\imath} + 2.0\hat{k} \text{ m}\) and velocity \(1.2 \hat{\imath} + 0.6 \hat{\jmath} \text{ m s}^{-1}\) in Galileo’s frame. Write down the time-dependent position of the book in the bird’s frame. What is the position vector, in the bird’s frame, that the book hits the ground?

You might find this much easier to solve if you draw a diagram with vectors showing the positions of the book and the bird relative to Galileo at time \(t\).

Using standard “SUVAT” equation for constant acceleration downwards from origin at top of tower \[ \vec{r} = -\frac{1}{2}gt^2 \hat{k} \]

The bird is initially at \(\vec{r}_0 = 3.1 \hat{\imath} + 2.0\hat{k} \text{ m}\) in Galileo’s frame and has velocity \(\vec{v} = 1.2 \hat{\imath} + 0.6 \hat{\jmath} \text{ m s}^{-1}\) relative to Galileo. This is most easily visualised with Figure 9.1.

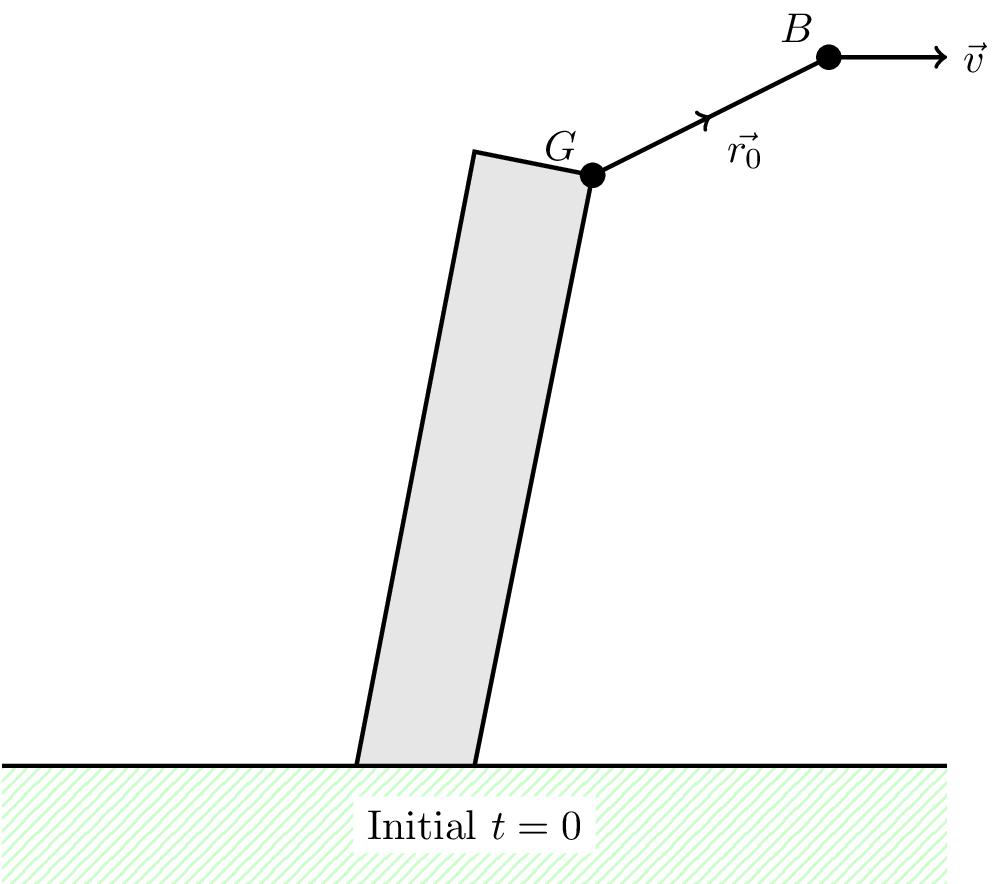
Figure 9.1: Initial condition at \(t=0\), with Galileo, \(G\), at the top of the tower and a bird, \(B\), flying by with velocity \(\vec{v}\). At this point Gelileo drops the book.

At some later time \(t > 0\) the book is at \(\vec{r}(t)\) in Galileo’s frame and \(\vec{r'}(t)\) in the bird’s frame.

At time \(t\) the bird is at \(\vec{r}_0 + \vec{v}t\) relative to Galileo’s frame. This is shown in Figure 9.2.

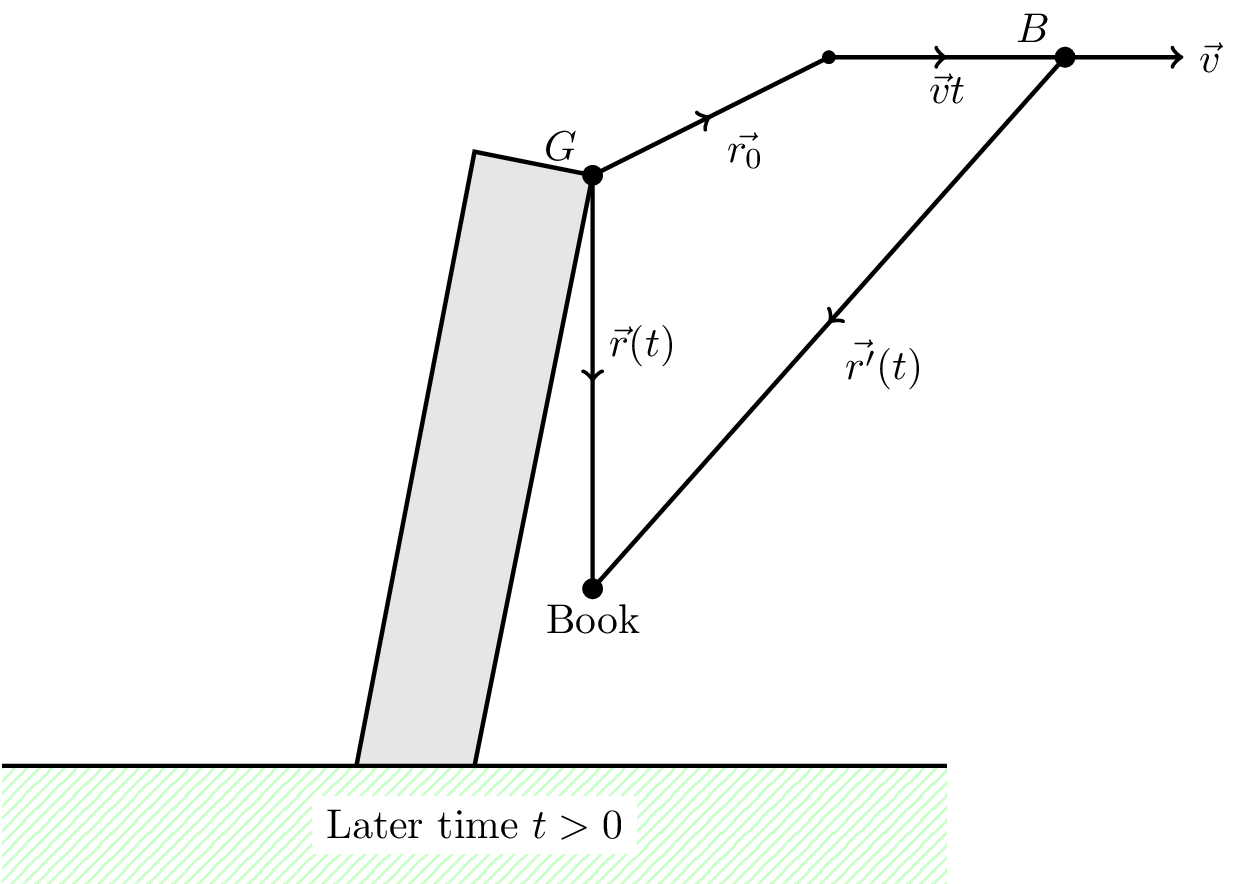
Figure 9.2: At some later time \(t > 0\), the book is falling vertically downwards. The bird, \(B\), has flown through a displacement \(\vec{v}t\).

From the diagram we can see that the book is at \[ \vec{r'}(t) = \vec{r}(t) - \vec{r}_0 - \vec{v}t \] relative to the bird. Substituting in the expression for \(\vec{r}(t)\) from part (a) gives \[ \vec{r'}(t) = -(3.1 + 1.2t) \hat{\imath} - 0.6t \hat{\jmath} - \left( 2.0 + \frac{gt^2}{2} \right) \hat{k} \] If the tower is 56 m high, the time to fall is 3.4 seconds, giving \[ \vec{r'}(t = 3.4) = -7.2 \hat{\imath} - 2.0 \hat{\jmath} - 58 \hat{k} \text{ m} \] for the landing position in the bird’s frame.